In my previous article, I discussed how to apply the baseball Pythagorean expectation to football and how to measure the error of the predictions using RMSE. This second article will demonstrate how to optimize the equation further to improve its accuracy.
One of the major reasons for the error in the predictions is the occurrence of draws in football. The Pythagorean expectation only looks at wins and losses and presumes that if a team scores zero goals then it will achieve zero points. This is of course incorrect, it is perfectly feasible for a team to fail to score but still gain a point through a nil-nil draw so we need to take this into account.
Howard Hamilton of Soccermetrics has published an updated Soccer Pythagorean equation that does just that, and it does a good job of it. For the 2011–2012 season, Howard Hamilton reports an RMSE of 3.81 compared with the RMSE of 5.65 I reported for my previous version of the Pythagorean equation. The downside to Howard Hamilton’s equation though is that it is rather complicated. While the original Pythagorean equation is simple enough to be used by any football fan, Howard Hamilton’s equation requires a decent understanding of mathematics to use it.
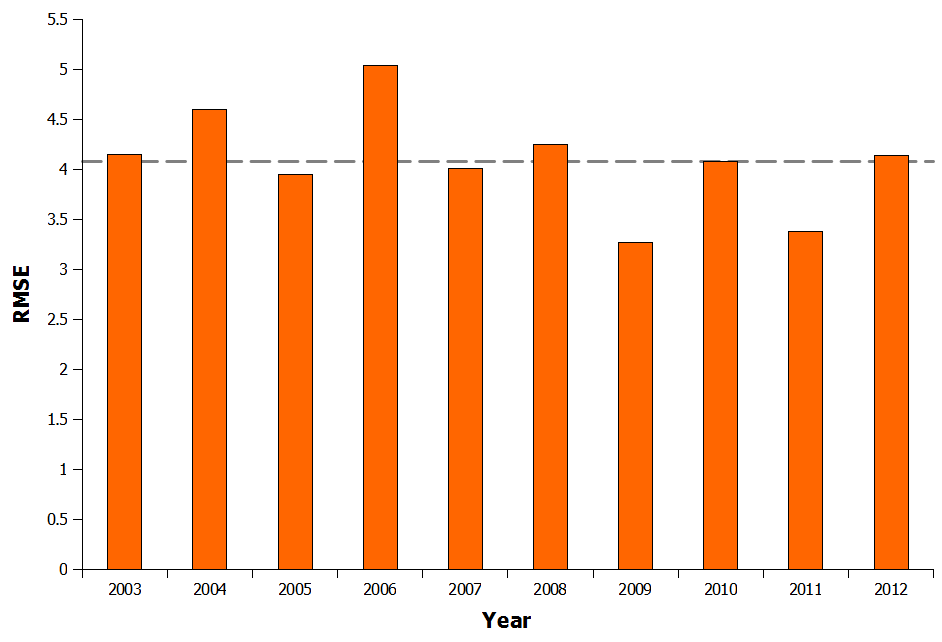
Because of that, I thought I would tweak the original Pythagorean formula a bit further to try and improve its accuracy without adding too much extra complexity to it. One easy way to do this is to scale the points scored per match to take into account the occurrence of draws. Applying least squares to this reduces the RMSE for the 2011–2012 season to 4.04 points, just 6% higher than Howard Hamilton’s equation. This is based on only one season’s data though so to get a true idea of how well my enhanced Pythagorean expectation works (abbreviated to MPE) I optimized the equation based on a much larger data set and applied it to the last 10 English Premier League (EPL) seasons ( Figure 1).
Figure 1: MPE Prediction by Season in the EPL
The MPE works well, with an average residual (the difference between predicted points and actual points) of 4.08 points. This compares nicely with Howard Hamilton’s published value of 3.81 and is less than half of the error the original Pythagorean Expectation equation gave. It is also worth noting that Howard Hamilton’s RMSE of 3.81 is for just one season, and of the ten seasons analysed here using the MPE, two actually have an RMSE lower than 3.81.
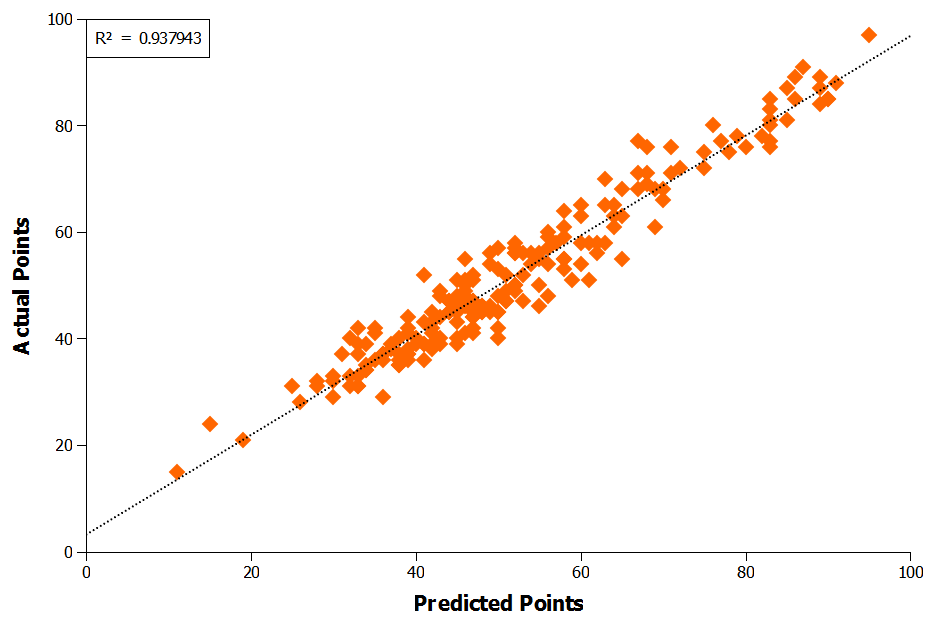
Plotting the MPE predicted points versus actual points for the last ten EPL seasons shows visually how well the MPE equation works (Figure 2). The correlation between the predicted and actual points scored is excellent, with an an r2 value 0.938 (Figure 2).
Figure 2: MPE Predicted Points Versus Actual Points in the EPL
So based on the initial work so far I am pleased that the MPE version of the Pythagorean expectation gives results comparable to Howard Hamilton’s more detailed and advanced derivation but without quite as much added complexity. The final equation for anybody who wants to give it a try is shown below in Figure 3.
Figure 3: MPE Equation